Le nombre d'or , la suite de Fibonacci et la peinture
Cette notion peut sembler étrange quand on y pense, mais les mathématiques et la peinture sont très étroitement liées. Bien que les mathématiques soient une science exacte et la peinture une activité artistique, nous avons remarqué que la peinture tient beaucoup des mathématiques. Sans oublier toutes les activités dérivées de la peinture que sont le dessin ou encore l’infographie.
En réalité, la construction d’une image et la notion de mise en valeur d’un point sur cette même image répondent à des règles mathématiques que tout élève en école d’art se doit de connaitre.
Comment ? Et qu’est-ce qui lie les cours de maths à la peinture ? C’est ce que nous allons voir tout de suite.
Les mathématiques appliquées à la peinture.
Un excellent exemple du lien entre les mathématiques et la peinture : le nombre d’or. Son histoire est une véritable saga qui court sur plusieurs millénaires.
Tout commence chez les Grecs où Pythagore étudiait tout ce qui était d’une grande beauté et sans défaut.
Les premières traces écrites du nombre d’or se trouvent dans les célèbres « Éléments » d’Euclide, mathématicien grec, (- 300) qui introduit la valeur particulière de 1,61803398875 (phi). Elle définit le “rectangle d’or” qui serait alors la représentation esthétique la plus harmonieuse.
C’est alors que l’on a mis en évidence une importante propriété du rectangle d’or.
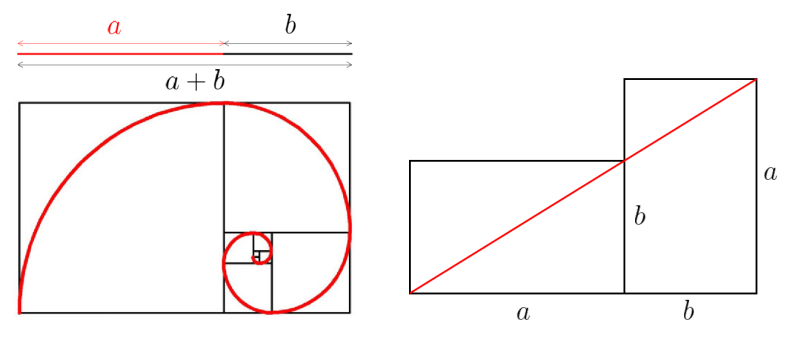
En effet, si on lui retranche un carré dont le côté est de la même longueur que celle de son petit côté, le nouveau rectangle est de nouveau un rectangle d’or. On peut alors tracer une spirale tangente au grand côté aux points de contact avec les carré ajoutés.
Définition :
- Le nombre d’or est défini comme le rapport a/b entre deux longueurs a et b.
- Ce rapport est tel que la somme a + b des deux longueurs est égale au rapport de la plus grande longueur (a) sur la plus petite (b).
- Mathématiquement, cela s’écrit : aa+b=ba
Valeur numérique :
- Le nombre d’or, noté φ (phi), est l’unique solution positive de l’équation φ² = φ + 1.
- Sa valeur approximative est 1,6180339887… (nombre irrationnel).
Dans la Rome Antique, les architectes, peintres, sculpteurs et dessinateurs ont compris la différence entre une œuvre esthétique et une création chaotique. Ils se sont intéressés à cette question et ont étudié comment une œuvre, bien qu’elles soient composées de parties inégales, peut être agréable à regarder. Ainsi, l’architecte romain Vitruve établit la définition du nombre d’or autrement dit la beauté mathématiques.
En reprenant à son compte le dessin de l'architecte Vitruve, Léonard de Vinci établit différentes mesures sur un corps humain, défini comme « parfait ». Parmi celles-ci, nous découvrons que, en étendant nos jambes, l’espace au sol ainsi créé et la figure formée par nos deux jambes forment un triangle équilatéral et que la longueur additionnée de nos deux bras tendus est égale à notre hauteur. De plus, ce dessin lui a permis de mesurer précisément chaque partie du corps, proportionnellement à notre corps tout entier. L’agencement de notre corps serait ainsi défini par ce fameux nombre d’or.
Ensuite, de nombreux mathématiciens dont le célèbre Léodarno de Pisa Fibonacci ont prouvé l’existence du nombre d’or dans la nature, chez les animaux et même chez l’homme. En 1175, il établit la suite de Fibonacci qui consiste à additionner les deux nombres précédents pour créer le troisième: 0,1,1,2,3,5,8,13,21,34,55,… Le rapport des deux termes consécutifs de la suite tend vers une valeur constante, Phi.
Mais revenons à la peinture. Il existe plusieurs figures tirant parti du nombre d’or. Nous pensons, par exemple, au rectangle d’or, à la spirale d’or, au triangle d’or, à l’ellipse d’or ou encore aux points d’or. Toutes ces données définissent précisément où doit se situer chaque élément d’un tableau, afin de rendre l’ensemble harmonieux et agréable à l’œil.
Les exemples les plus flagrants de l’utilisation du nombre d’or dans la peinture sont :
- La naissance de Vénus, peinte par Sandro Botticelli en 1482. En observant ce tableau, nous remarquons que la position dans l’espace des personnages est soumise à la règle des rectangles d’or. D’ailleurs, le tableau en lui-même est un rectangle d’or dans son ensemble. Ses dimensions (172,5 cm sur 278,05 cm) correspondent exactement aux formats d’un rectangle d’or.
- Le tableau de Jicopo de Barbari représentant le mathématicien Fra Luca Pacioli possède, en son sein, une représentation parfaite de l’utilisation du nombre d’or. Celle-ci se situe dans la relation et la distance qui existe entre l’index et le pouce de la main correspondant exactement à la hauteur du livre ouvert. D’ailleurs, ce mathématicien écrivit en 1498 un traité sur le nombre d’or. Cette représentation n’est donc pas anodine.
- Sans oublier le tableau de Diego Velazquez, l’adoration des Mages, peint en 1609. Comme la Naissance de Vénus, le format du tableau en lui-même est un rectangle d’or. De plus, le visage de Jésus enfant est situé exactement sur un point d’or.
Génie des mathématiques et de la peinture : Léonard de Vinci
Une des plus grandes figures dans le domaine de l’art, des mathématiques et de l’ingénierie est sans conteste Léonard de Vinci, véritable génie, inventeur et artiste. Nous lui devons la notion de la perspective, ayant servi à un grand nombre d’artistes aujourd’hui encore.
En tant que mathématicien, Léonard de Vinci connait le nombre d’or et l’utilise, à son tour, dans de nombreuses peintures. Dans le tableau de La Joconde, par exemple, le visage de La Joconde s’insère parfaitement dans un rectangle d’or. Idem pour la proportion de son corps, qui de coude à coude, rentre aussi dans un rectangle d’or.
Autre œuvre de Léonard de Vinci qui utilise la règle des rectangles d’or : Le Repas du Seigneur, peint entre 1494 et 1497. Cette œuvre a été créée en utilisant des rectangles d’or mais aussi de nombreuses figures géométriques.
C’est un fait, Léonard de Vinci, pour peindre ses chefs-d’œuvre, utilisa énormément les théorèmes mathématiques les plus connus de son temps. Cela apporta à ses tableaux une véritable harmonie.
Aujourd’hui encore, nous étudions ses œuvres de façon à identifier les différents stratagèmes utilisés pour peindre ses tableaux, reconnus comme des classiques de l’histoire de l’art.
Les propriétés de la divine proportion se retrouvent donc dans l’esthétique.
C’est un critère de beauté que l’on observe en peinture.
Les logos aux divines proportions
Un grand nombre de logos suive ce fil conducteur mathématique pour devenir plus efficaces, plus équilibrés et plus convaincants.
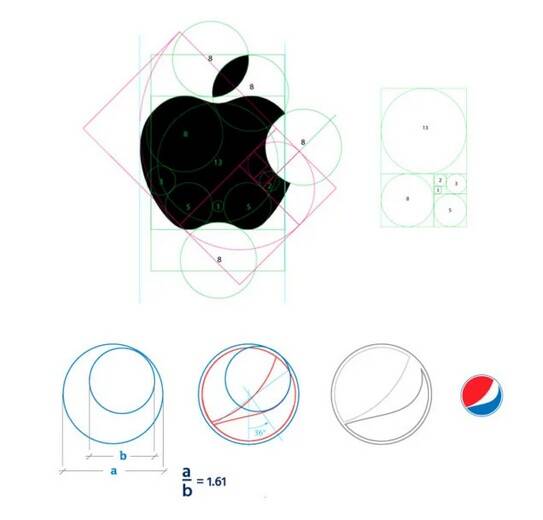
Exemples des logos qui sont construits grâce à la suite de Fibonacci : le logo d’Apple de Rob Janoff, le logo BP, Grupo Boticario, National Geographic, Pepsi, Toyota
On comprend mieux pourquoi dans la photographie, la composition d’un visuel ou d’un logo on retrouve la technique de la règle des tiers pour la photographie et la grille d’or en infographie.
